Given a Grammar Draw the Tree Fractal

Creating fractals with Python

Try it yourself in this post!

Fractal art — source

First of all, what is a geometric fractal? A geometric fractal is a geometric shape with a repeating structure at different scales: it doesn't matter whether you get closer to the image or not, you'll always see the same pattern. Or, as defined by Benoit Mandelbrot, "a rough or fragmented geometric shape that can be split into parts, each of which is (at least approximately) a reduced-size copy of the whole".

Now, how can we build a fractal in Python? Given that we are repeating a structure at different scales, we'll need to apply a recursive solution. Moreover, we'll be using turtle to draw the fractals. In this post, we'll be drawing both a fractal tree and a Koch snowflake.

Drawing a fractal tree

In order to create a tree, we are going to divide each branch into two sub-branches (left and right) and shorten the new sub-branches, until we reach a minimum branch length, defined by ourselves:

          import turtle          MINIMUM_BRANCH_LENGTH = 5          def build_tree(t, branch_length, shorten_by, angle):
            pass          tree = turtle.Turtle()
tree.hideturtle()
tree.setheading(90)
tree.color('green')          build_tree(tree, 50, 5, 30)
turtle.mainloop()        

So far, we've just defined the basics. We've imported turtle and created an instance of turtle.Turtle(), which will be the object moving around the canvas and drawing our tree. We've then made it face upwards with setheading(). We've also defined the signature of our recursive function, which will be the following:

• t: our Turtle instance.
• branch_length: the current length of the branch in pixels.
• shorten_by: determines by how many pixels the sub-branches will be shorter than the parent branch.
• angle: the angles from which the sub-branches emerge from the parent branch.

Moreover, we've defined the MINIMUM_BRANCH_LENGTH (in pixels), which sets the minimum threshold to create further sub-branches.

Let's now build the body of our recursive function:

          import turtle          MINIMUM_BRANCH_LENGTH = 5          def build_tree(t, branch_length, shorten_by, angle):
            if branch_length > MINIMUM_BRANCH_LENGTH:
            t.forward(branch_length)
            new_length = branch_length - shorten_by                      t.left(angle)
            build_tree(t, new_length, shorten_by, angle)                      t.right(angle * 2)
            build_tree(t, new_length, shorten_by, angle)                      t.left(angle)
            t.backward(branch_length)          tree = turtle.Turtle()
tree.hideturtle()
tree.setheading(90)
tree.color('green')          build_tree(tree, 50, 5, 30)
turtle.mainloop()        

As you can see, we reach our base case if branch_length is lower than MINIMUM_BRANCH_LENGTH. Otherwise, we draw the branch and proceed to create the sub-branches by computing their length and turning left and right by "angle" degrees and calling build_tree again with the new values. Finally, we move backwards to the root of our branch.

If you execute the code you should obtain the following result:

Our fractal tree

Finally, feel free to play around with the code (and the parameters) here!

Drawing a Koch snowflake

In the second section of this post we'll be drawing a more complex structure: the Koch snowflake.

First of all, we'll need to create a recursive function to create the Koch curve, and then we'll be joining 3 of these curves to create a snowflake. Let's start by defining the parameters of our recursive function:

• t: our Turtle instance.
• iterations: represents the value of n in the image below this list (note that n=0 would represent a flat line, which will be the base case in our recursive function).
• length: the length of each side in our current (sub-)snowflake.
• shortening_factor: determines the factor by which the side length is divided when we create a new sub-snowflake.
• angle: determines the angle from which the new side emerges.

Koch curve construction — source

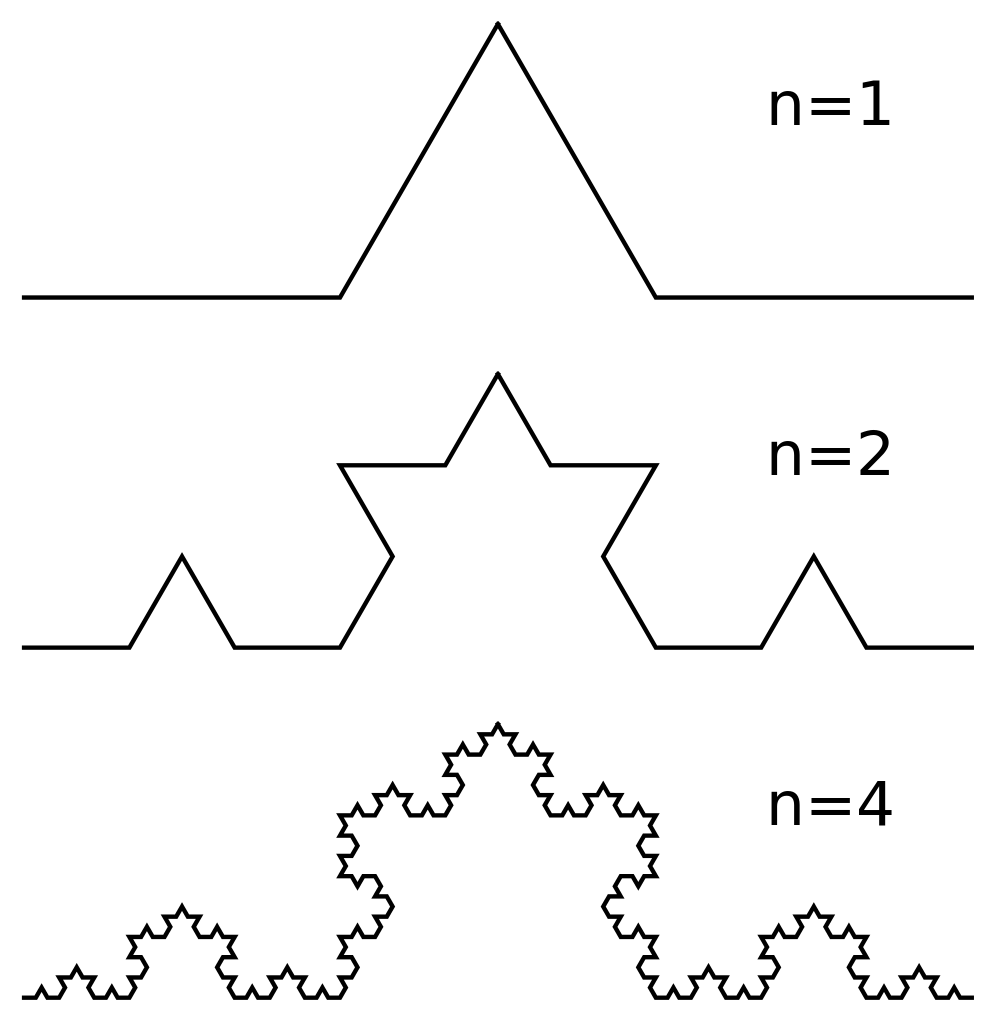
Once we have defined the basic structure of our recursive function, we may reach the following point:

          import turtle          def koch_curve(t, iterations, length, shortening_factor, angle):
            pass          t = turtle.Turtle()
t.hideturtle()          for i in range(3):
            koch_curve(t, 4, 200, 3, 60)
            t.right(120)          turtle.mainloop()        

At this point, we just have to implement the recursive function. If we have reached our base case, we'll just draw a line. Otherwise, we'll update our parameters (specifically, iterations and length) and call our recursive function 4 times. Between these function calls we'll be turning first to the left, then to the right and finally to the left again. Let's see how the full implementation looks:

          import turtle          def koch_curve(t, iterations, length, shortening_factor, angle):                      if iterations == 0:
            t.forward(length)
            else:
            iterations = iterations - 1
            length = length / shortening_factor                      koch_curve(t, iterations, length, shortening_factor, angle)
            t.left(angle)
            koch_curve(t, iterations, length, shortening_factor, angle)
            t.right(angle * 2)
            koch_curve(t, iterations, length, shortening_factor, angle)
            t.left(angle)
            koch_curve(t, iterations, length, shortening_factor, angle)          t = turtle.Turtle()
t.hideturtle()          for i in range(3):
            koch_curve(t, 4, 200, 3, 60)
            t.right(120)          turtle.mainloop()        

If you execute the code above, you should obtain the following result:

Our Koch snowflake

Again, feel free to play around with the code (and parameters) here!

massieporchish.blogspot.com

Source: https://towardsdatascience.com/creating-fractals-with-python-d2b663786da6

Share this post